Tree Recursion
- Press O or Escape for overview mode.
- Press the copy icon on the upper right of code blocks to copy the code
Class outline:
- Order of recursive calls
- Tree recursion
- Counting partitions
Order of recursive calls
The cascade function
def cascade(n):
if n < 10:
print(n)
else:
print(n)
cascade(n//10)
print(n)
What would this display?
cascade(123)
Cascade environment diagram
def cascade(n):
if n < 10:
print(n)
else:
print(n)
cascade(n//10)
print(n)
cascade(123)
- Each cascade frame is from a different call to cascade.
- Until the Return value appears, that call has not completed.
- Any statement can appear before or after the recursive call.
| cascade | → func cascade(n)[parent=Global] |
| n | 123 | |
| Return value | None |
| n | 12 | |
| Return value | None |
| n | 1 | |
| Return value | None |
123
12
1
12
123
Two definitions of cascade
def cascade(n):
if n < 10:
print(n)
else:
print(n)
cascade(n//10)
print(n)
def cascade(n):
print(n)
if n >= 10:
cascade(n//10)
print(n)
- If two implementations are equally clear, then the shorter one is usually better
- When learning to write recursive functions, put the base cases first
- Both are recursive functions, even though only the first has typical structure
Inverse cascade
How can we output this cascade instead?
1
12
123
12
1
Inverse cascade solution
def inverse_cascade(n):
grow(n)
print(n)
shrink(n)
def f_then_g(f, g, n):
if n:
f(n)
g(n)
grow = lambda n: f_then_g(grow, print, n//10)
shrink = lambda n: f_then_g(print, shrink, n//10)
Tree recursion
Tree Recursion
Tree-shaped processes arise whenever a recursive function makes more than one recursive call.
Recursive Virahanka-Fibonacci
The nth number is defined as:
$$\small\begin{equation*} \text{virfib}(n) = \begin{cases} 0 & \text{if } n = 0 \\ 1 & \text{if } n = 1 \\ \text{virfib}(n - 1) + \text{virfib}(n - 2) & \text{otherwise} \\ \end{cases} \end{equation*}$$
def virfib(n):
"""Compute the nth Virahanka-Fibonacci number, for N >= 1.
>>> virfib(2)
1
>>> virfib(6)
8
"""
if n == 0:
return 0
elif n == 1:
return 1
else:
return virfib(n-2) + virfib(n-1)
A tree-recursive process
Redundant computations
The function is called on the same number multiple times. 🙀
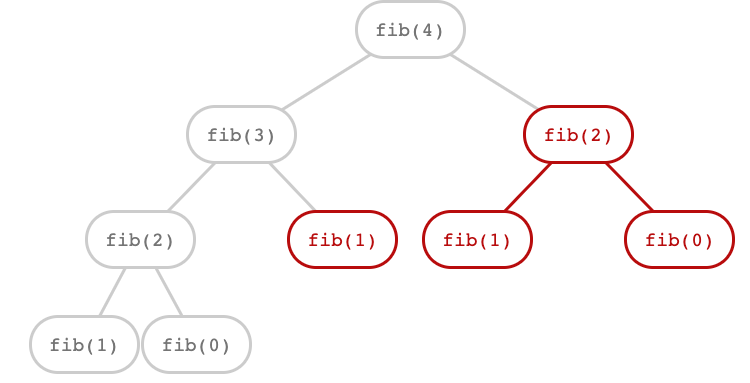
(We will speed up this computation dramatically in a few weeks by remembering results)
Counting partitions
Counting partitions problem
The number of partitions of a positive integer n, using parts up to size m, is the number
of ways in which n can be expressed as the sum of positive integer parts up to m in
increasing order.
count_partitions(6, 4)
| 2 + 4 = 6 | |||||||||||
| 1 + 1 + 4 = 6 | |||||||||||
| 3 + 3 = 6 | |||||||||||
| 1 + 2 + 3 = 6 | |||||||||||
| 1 + 1 + 1 + 3 = 6 | |||||||||||
| 2 + 2 + 2 = 6 | |||||||||||
| 1 + 1 + 2 + 2 = 6 | |||||||||||
| 1 + 1 + 1 + 1 + 2 = 6 | |||||||||||
| 1 + 1 + 1 + 1 + 1 + 1 = 6 |
Counting partitions approach
The number of partitions of a positive integer n, using parts up to size m, is the number
of ways in which n can be expressed as the sum of positive integer parts up to m in
increasing order.
count_partitions(6, 4)
Recursive decomposition: finding simpler instances of the problem.
Explore two possibilities:
- Use at least one 4
- Don't use any 4
Tree recursion often involves exploring different choices.
Counting partitions approach
The number of partitions of a positive integer n, using parts up to size m, is the number
of ways in which n can be expressed as the sum of positive integer parts up to m in
increasing order.
count_partitions(6, 4)
Solve two simpler problems:
count_partitions(2, 4) |
|||||||||||
count_partitions(n-m, m) |
|||||||||||
count_partitions(6, 3) |
|||||||||||
count_partitions(n, m-1) |
|||||||||||
Counting partitions code
The number of partitions of a positive integer n, using parts up to size m, is the number
of ways in which n can be expressed as the sum of positive integer parts up to m in
increasing order.
count_partitions(6, 4)
Solve two simpler problems:
with parts of size m:
count_partitions(2, 4)count_partitions(n-m, m)without parts of size m:
count_partitions(6, 3)count_partitions(n, m-1)
def count_partitions(n, m):
"""
>>> count_partitions(6, 4)
9
"""
if n == 0:
return 1
elif n < 0:
return 0
elif m == 0:
return 0
else:
with_m = count_partitions(n-m, m)
without_m = count_partitions(n, m-1)
return with_m + without_m