Sequences
- Press O or Escape for overview mode.
- Press the copy icon on the upper right of code blocks to copy the code
Class outline:
- Box+Pointer
- Slicing
- Recursive exercises
- Built-ins for iterables
Box + Pointer
Lists in environment diagrams
Lists are represented as a row of index-labeled adjacent boxes, one per element.
pair = [1, 2]
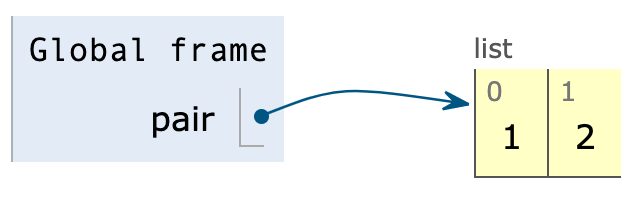
Nested lists in environment diagrams
Each box either contains a primitive value or points to a compound value.
matrix = [ [1,2,0,4], [0,1,3,-1], [0,0,1,8] ]
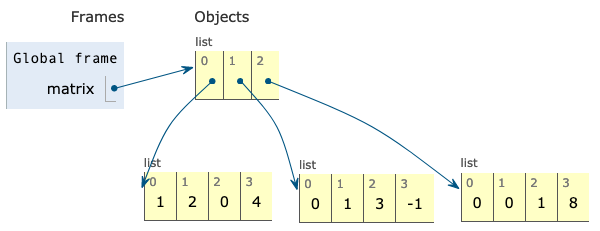
Nested lists in environment diagrams
A very nested list:
nested_list = [ [1, 2],
[],
[ [3, False, None],
[4, lambda: 5]]]
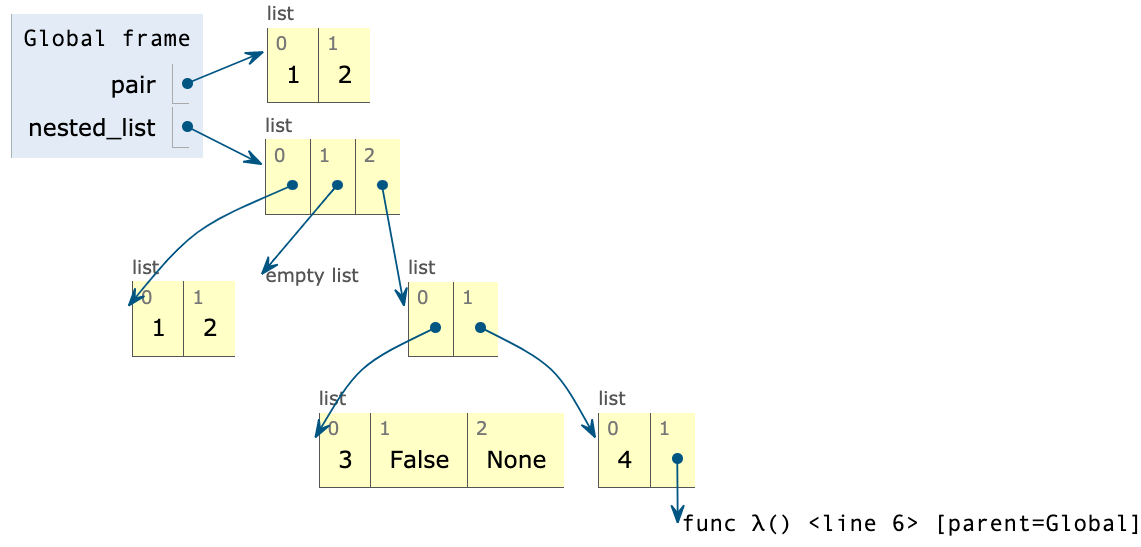
Slicing
Slicing syntax
Slicing a list creates a new list with a subsequence of the original list.
letters = ["A", "B", "C", "D", "E", "F"]
# 0 1 2 3 4 5
sublist1 = letters[1:] # ['B', 'C', 'D', 'E', 'F']
sublist2 = letters[1:4] # ['B', 'C', 'D']
Slicing also works for strings.
compound_word = "cortaúñas"
word1 = compound_word[:5] # "corta"
word2 = compound_word[5:] # "úñas"
Negatives indices and steps can also be specified.
Copying whole lists
Slicing a whole list copies a list:
listA = [2, 3]
listB = listA
listC = listA[:]
listA[0] = 4
listB[1] = 5
list() creates a new list containing existing elements from any
iterable:
listA = [2, 3]
listB = listA
listC = list(listA)
listA[0] = 4
listB[1] = 5
Python3 provides more ways in the copy module.
Recursion exercises
Recursively sum a list
Let's code this up recursively:
def sum_nums(nums):
"""Returns the sum of the numbers in nums.
>>> sum_nums([6, 24, 1984])
2014
>>> sum_nums([-32, 0, 32])
0
"""
Docstrings typically would not specify whether an approach was recursive or iterative, since that is an implementation detail.
However, we'll make it clear in assignments and exam questions.
Recursively sum a list (solution)
def sum_nums(nums):
"""Returns the sum of the numbers in nums.
>>> sum_nums([6, 24, 1984])
2014
>>> sum_nums([-32, 0, 32])
0
"""
if nums == []:
return 0
else:
return nums[0] + sum_nums( nums[1:] )
When recursively processing lists, the base case is often the empty list and the recursive case is often all-but-the-first items.
Iteratively sum a range
Let's code this up iteratively:
def sum_up_to(n):
"""Returns the sum of positive numbers from 1 up to n (inclusive).
>>> sum_up_to(5)
15
"""
Iteratively sum a range (solution)
Using the range type:
def sum_up_to(n):
"""Returns the sum of positive numbers from 1 up to n (inclusive).
>>> sum_up_to(5)
15
"""
sum = 0
for n in range(0, n+1):
sum += n
return sum
Remember that range(start, end) always ends right before
end.
Recursively sum a range
Now try it recursively:
def sum_up_to(n):
"""Returns the sum of positive numbers from 1 up to n (inclusive).
>>> sum_up_to(5)
15
"""
Recursively sum a range (solution)
Now try it recursively:
def sum_up_to(n):
"""Returns the sum of positive numbers from 1 up to n (inclusive).
>>> sum_up_to(5)
15
"""
if n == 1:
return 1
else:
return n + sum_up_to(n-1)
Reversing a string
Recursively reversing a string
def reverse(s):
"""Returns a string with the letters of s
in the inverse order.
>>> reverse('ward')
'draw'
"""
Breaking it down into subproblems:
reverse("ward") = reverse("ard") + "w"
reverse("ard") = reverse("rd") + "a"
reverse("rd") = reverse("d") + "r"
reverse("d") = "d"
Recursively reversing a string (solution)
def reverse(s):
"""Returns a string with the letters of s
in the inverse order.
>>> reverse('ward')
'draw'
"""
if len(s) == 1:
return s
else:
return reverse(s[1:]) + s[0]
When recursively processing strings, the base case is typically an empty string or single-character string, and the recursive case is often all-but-the-first characters.
Recursively reversing a string (visual)
Exercise: Reversing a number
def reverse_digits(n):
"""Returns n with the digits reversed.
>>> reverse_digits(123)
321
"""
Exercise: Reversing a number (solution)
def reverse_digits(n):
"""Returns n with the digits reversed.
>>> reverse_digits(123)
321
"""
def reverse(n, r):
r *= 10
if n < 10:
return r + n
else:
return reverse(n // 10, r + n % 10)
return reverse(n, 0)
Helper functions
If a recursive function needs to keep track of more state than the arguments of the original function, you may need a helper function.
def fUnKyCaSe(text):
"""Returns text in fUnKyCaSe
>>> fUnKyCaSe("wats up")
'wAtS Up'
"""
def toggle_case(letter, should_up_case):
return letter.upper() if should_up_case else letter.lower()
def up_down(text, should_up_case):
if len(text) == 1:
return toggle_case(text, should_up_case)
else:
return toggle_case(text[0], should_up_case) + up_down(text[1:], not should_up_case)
return up_down(text, False)
Recursion on different data types
| Data type | Base case condition | Current item | Recursive case argument |
|---|---|---|---|
| Numbers |
== 0 == 1
|
n % 10 |
n // 10 |
| Lists | == [] |
L[0] |
L[1:] L[:-1]
|
| Strings |
== '' len(S) == 1
|
S[0] |
S[1:] S[:-1]
|
Built-in functions for iterables
Functions that process iterables
The following built-in functions work for sequence types (lists, strings, etc) and any other iterable data type.
| Function | Description |
|---|---|
sum(iterable, start) |
Returns the sum of values in iterable, initializing sum
to start
|
all(iterable)
|
Return True if all elements of iterable are
true (or if iterable is empty)
|
any(iterable)
|
Return True if any element of iterable is
true. Return False if iterable is empty.
|
max(iterable, key=None) |
Return the max value in iterable
|
min(iterable, key=None) |
Return the min value in iterable
|
Examples with sum/any/all
sum([73, 89, 74, 95], 0) # 331
all([True, True, True, True]) # True
any([False, False, False, True]) # True
all([x < 5 for x in range(5)]) # True
perfect_square = lambda x: x == round(x ** 0.5) ** 2
any([perfect_square(x) for x in range(50, 60)]) # False
Examples with max/min
max([73, 89, 74, 95]) # 95
max(["C+", "B+", "C", "A"]) # C+
max(range(10)) # 9
A key function can decide how to compare each value:
coords = [ [37, -144], [-22, -115], [56, -163] ]
max(coords, key=lambda coord: coord[0]) # [56, -163]
min(coords, key=lambda coord: coord[0]) # [-22, -115]
gymnasts = [ ["Brittany", 9.15, 9.4, 9.3, 9.2],
["Lea", 9, 8.8, 9.1, 9.5],
["Maya", 9.2, 8.7, 9.2, 8.8] ]
min(gymnasts, key=lambda scores: min(scores[1:])) # ["Maya", ...]
max(gymnasts, key=lambda scores: sum(scores[1:], 0)) # ["Brittany", ...]