Trees
- Press O or Escape for overview mode.
- Press the copy icon on the upper right of code blocks to copy the code
Class outline:
- Trees 🌴🌳🌲
Trees
Trees
| Recursive description | Relative description |
|---|---|
|
|
Trees: Data abstraction
We want this constructor and selectors:
tree(label, branches)
|
Returns a tree with root label and list of
branches
|
label(tree) |
Returns the root label of tree |
branches(tree) |
Returns the branches of tree (each a tree). |
is_leaf(tree) |
Returns true if tree is a leaf node. |
t = tree(3, [
tree(1),
tree(2, [
tree(1),
tree(1)
])])
label(t) # 3
is_leaf(branches(t)[0]) # True
Tree: Our implementation
t = tree(3, [
tree(1),
tree(2, [
tree(1),
tree(1)
])])
Each tree is stored as a list where first element is label and subsequent elements are branches.
[3, [1], [2, [1], [1]]]
def tree(label, branches=[]):
return [label] + list(branches)
def label(tree):
return tree[0]
def branches(tree):
return tree[1:]
def is_leaf(tree):
return len(branches(tree)) == 0
Trees: Dict Implementation
A dictionary for each tree/subtree:
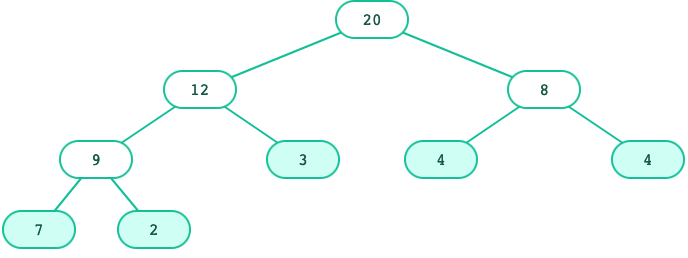
{'l':20,'c':[{'l':12,'c':[{'l':9,'c':[{'l':7,'c':
[]},{'l':2,'c':[]}]},{'l':3,'c':[]}]},{'l':8,'c':[{'l':4,'c':[]},{'l':4,'c':[]}]}]}
def tree(label, branches=[]):
return {"l": label, "b": branches}
def label(tree):
return tree["l"]
def branches(tree):
return tree["b"]
t = tree(20, [tree(12,
[tree(9,
[tree(7), tree(2)]),
tree(3)]),
tree(8,
[tree(4), tree(4)])])
Tree processing
A tree is a recursive structure.
Each tree has:
- A label
- 0 or more branches, each a tree
Recursive structure implies recursive algorithm!
Tree processing: Counting leaves

def count_leaves(t):
"""Returns the number of leaf nodes in t."""
if is_leaf(t):
return 1
else:
leaves_under = 0
for b in branches(t):
leaves_under += count_leaves(b)
return leaves_under
What's the base case? What's the recursive call?
Tree processing: Counting leaves
The
sum()
function sums up the items of an iterable.
sum([1, 1, 1, 1]) # 4
That leads to this shorter function:
def count_leaves(t):
"""Returns the number of leaf nodes in t."""
if is_leaf(t):
return 1
else:
branch_counts = [count_leaves(b) for b in branches(t)]
return sum(branch_counts)
Creating trees
A function that creates a tree from another tree is also often recursive.
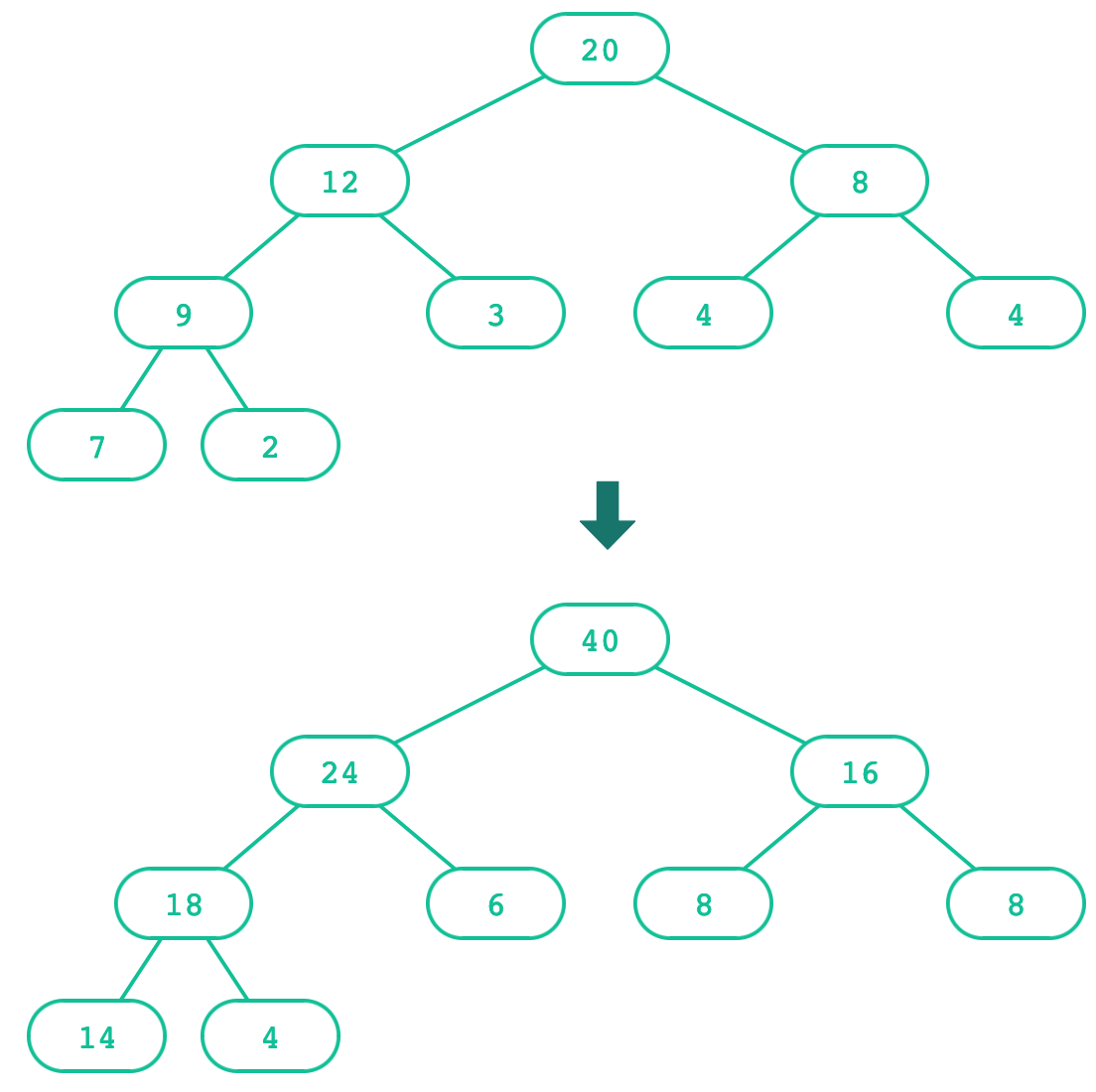
Creating trees: Doubling labels

def double(t):
"""Returns a tree identical to t, but with all labels doubled."""
if is_leaf(t):
return tree(label(t) * 2)
else:
return tree(label(t) * 2,
[double(b) for b in branches(t)])
What's the base case? What's the recursive call?
Creating trees: Doubling labels
A shorter solution:
def double(t):
"""Returns the number of leaf nodes in t."""
return tree(label(t) * 2,
[double(b) for b in branches(t)])
Explicit base cases aren't always necessary in the final code, but it's useful to think in terms of base case vs. recursive case when learning.
Exercise: Printing trees
def print_tree(t, indent=0):
"""Prints the labels of t with a depth-based indent of 2 spaces.
>>> t = tree(3, [tree(1), tree(2, [tree(1), tree(1)])])
>>> print(t)
3
1
2
1
1
"""
Exercise: Printing trees (solution)
def print_tree(t, indent=0):
"""Prints the labels of t with a depth-based indent of 2 spaces.
>>> t = tree(3, [tree(1), tree(2, [tree(1), tree(1)])])
>>> print(t)
3
1
2
1
1
"""
print(indent * " " + label(t))
for b in branches(t):
print_tree(b, indent + 2)
Exercise: List of leaves
def leaves(t):
"""Return a list containing the leaf labels of t.
>>> t = tree(20, [tree(12, [tree(9, [tree(7), tree(2)]), tree(3)]), tree(8, [tree(4), tree(4)])])
>>> leaves(t)
[7, 2, 3, 4, 4]
"""
Hint: If you sum a list of lists, you get a list containing the elements of those lists. The sum function takes a second argument, the starting value of the sum.
sum([ [1], [2, 3], [4] ], []) # [1, 2, 3, 4]
sum([ [1] ], []) # [1]
sum([ [[1]], [2] ], []) # [[1], 2]
Exercise: List of leaves (Solution)
def leaves(t):
"""Return a list containing the leaf labels of t.
>>> t = tree(20, [tree(12, [tree(9, [tree(7), tree(2)]), tree(3)]), tree(8, [tree(4), tree(4)])])
>>> leaves(t)
[7, 2, 3, 4, 4]
"""
if is_leaf(t):
return [label(t)]
else:
leaf_labels = [leaves(b) for b in branches(t)]
return sum(leaf_labels, [])
Exercise: Counting paths
def count_paths(t, total):
"""Return the number of paths from the root to any node in t
for which the labels along the path sum to total.
>>> t = tree(3, [tree(-1), tree(1, [tree(2, [tree(1)]), tree(3)]), tree(1, [tree(-1)])])
>>> count_paths(t, 3)
2
>>> count_paths(t, 4)
2
>>> count_paths(t, 5)
0
>>> count_paths(t, 6)
1
>>> count_paths(t, 7)
2
"""
Exercise: Counting paths (solution)
def count_paths(t, total):
"""Return the number of paths from the root to any node in t
for which the labels along the path sum to total.
>>> t = tree(3, [tree(-1), tree(1, [tree(2, [tree(1)]), tree(3)]), tree(1, [tree(-1)])])
>>> count_paths(t, 3)
2
>>> count_paths(t, 4)
2
>>> count_paths(t, 5)
0
>>> count_paths(t, 6)
1
>>> count_paths(t, 7)
2
"""
if label(t) == total:
found = 1
else:
found = 0
return found + sum([count_paths(b, total - label(t)) for b in branches(t)])
Tree: Layers of abstraction
| Primitive Representation |
1 2 3"a" "b" "c"[..,..]
|
| Data abstraction |
tree() branches() label()
|
is_leaf() |
|
| User program | double(t) count_leaves(t) |
Each layer only uses the layer above it.
Trees, trees, everywhere!
Directory structures

Parse trees
For natural languages...

Key: S = Sentence, NP = Noun phrase, D = Determiner, N = Noun, V = Verb, VP = Verb Phrase
Parse trees
For programming languages, too...
