Recursive Objects
- Press O or Escape for overview mode.
- Press the copy icon on the upper right of code blocks to copy the code
Class outline:
- Linked Lists
- Link class
- Tree class
Linked lists
Why do we need a new list?
Python lists are implemented as a "dynamic array", which isn't optimal for all use cases.
😭 Inserting an element is slow, especially near front of list:
😭 Plus inserting too many elements can require re-creating the entire list in memory, if it exceeds the pre-allocated memory.
Linked lists
A linked list is a chain of objects where each object holds a value and a reference to the next link. The list ends when the final reference is empty.
Linked lists require more space but provide faster insertion.
Performance Comparison
timeit.timeit(lambda: f(range(10,000)), number=10)
| Operation | Linked List | list | list advantage |
| Insert at head | 0.0249 | 0.1235 | 0.23 |
| Insert at mid | 18.985 | 0.0630 | 296. |
| Insert at end | 24.429 | 0.0025 | 10187. |
| Search mid | 0.0251 | 0.0015 | 16. |
| Index mid | 0.02556 | 0.00113 | 21. |
| Length | 0.02968 | 0.00116 | 23. |
| Sum | 0.03016 | 0.00184 | 16. |
Linked lists require more space and provide slower insertion and transversal.
A Link class
class Link:
empty = ()
def __init__(self, first, rest=empty):
self.first = first
self.rest = rest
How would we use that?
ll = Link("A", Link("B", Link("C")))
A fancier LinkedList
class Link:
"""A linked list."""
empty = ()
def __init__(self, first, rest=empty):
assert rest is Link.empty or isinstance(rest, Link)
self.first = first
self.rest = rest
def __repr__(self):
if self.rest:
rest_repr = ', ' + repr(self.rest)
else:
rest_repr = ''
return 'Link(' + repr(self.first) + rest_repr + ')'
def __str__(self):
string = '<'
while self.rest is not Link.empty:
string += str(self.first) + ' '
self = self.rest
return string + str(self.first) + '>'
Creating linked lists
Creating a range
Similar to [x for x in range(3, 6)]
def range_link(start, end):
"""Return a Link containing consecutive integers
from start to end, not including end.
>>> range_link(3, 6)
Link(3, Link(4, Link(5)))
"""
if start >= end:
return Link.empty
return Link(start, range_link(start + 1, end))
Exercise: Mapping a linked list
Similar to [f(x) for x in lst]
def map_link(f, ll):
"""Return a Link that contains f(x) for each x in Link LL.
>>> square = lambda x: x * x
>>> map_link(square, range_link(3, 6))
Link(9, Link(16, Link(25)))
"""
Exercise: Mapping a linked list (Solution)
Similar to [f(x) for x in lst]
def map_link(f, ll):
"""Return a Link that contains f(x) for each x in Link LL.
>>> square = lambda x: x * x
>>> map_link(square, range_link(3, 6))
Link(9, Link(16, Link(25)))
"""
if ll is Link.empty:
return Link.empty
return Link(f(ll.first), map_link(f, ll.rest))
Exercise: Filtering a linked list
Similar to [x for x in lst if f(x)]
def filter_link(f, ll):
"""Return a Link that contains only the elements x of Link LL
for which f(x) is a true value.
>>> is_odd = lambda x: x % 2 == 1
>>> filter_link(is_odd, range_link(3, 6))
Link(3, Link(5))
"""
Exercise: Filtering a linked list (Solution)
Similar to [x for x in lst if f(x)]
def filter_link(f, ll):
"""Return a Link that contains only the elements x of Link LL
for which f(x) is a true value.
>>> is_odd = lambda x: x % 2 == 1
>>> filter_link(is_odd, range_link(3, 6))
Link(3, Link(5))
"""
if ll is Link.empty:
return Link.empty
elif f(ll.first):
return Link(ll.first, filter_link(f, ll.rest))
return filter_link(f, ll.rest)
Mutating linked lists
Linked lists can change
Attribute assignments can change first and
rest attributes of a Link.
s = Link("A", Link("B", Link("C")))
s.first = "Hi"
s.rest.first = "Hola"
s.rest.rest.first = "Oi"
Beware infinite lists
The rest of a linked list can contain the linked list as a sub-list.
s = Link("A", Link("B", Link("C")))
t = s.rest
t.rest = s
s.first # 'A'
s.rest.rest.rest.rest.rest.first # 'B'
Exercise: Adding to front of linked list
def insert_front(linked_list, new_val):
"""Inserts new_val in front of linked_list,
returning new linked list.
>>> ll = Link(1, Link(3, Link(5)))
>>> insert_front(ll, 0)
Link(0, Link(1, Link(3, Link(5))))
"""
Exercise: Adding to front of linked list (Solution)
def insert_front(linked_list, new_val):
"""Inserts new_val in front of linked_list,
returning new linked list.
>>> ll = Link(1, Link(3, Link(5)))
>>> insert_front(ll, 0)
Link(0, Link(1, Link(3, Link(5))))
"""
return Link(new_val, linked_list)
Exercise: Adding to an ordered linked list
def add(ordered_list, new_val):
"""Add new_val to ordered_list, returning modified ordered_list.
>>> s = Link(1, Link(3, Link(5)))
>>> add(s, 0)
Link(0, Link(1, Link(3, Link(5))))
>>> add(s, 3)
Link(0, Link(1, Link(3, Link(5))))
>>> add(s, 4)
Link(0, Link(1, Link(3, Link(4, Link(5)))))
>>> add(s, 6)
Link(0, Link(1, Link(3, Link(4, Link(5, Link(6))))))
"""
if new_val < ordered_list.first:
elif new_val > ordered_list.first and ordered_list.rest is Link.empty:
elif new_val > ordered_list.first:
return ordered_list
Exercise: Adding to an ordered linked list (Solution)
def add(ordered_list, new_val):
"""Add new_val to ordered_list, returning modified ordered_list.
>>> s = Link(1, Link(3, Link(5)))
>>> add(s, 0)
Link(0, Link(1, Link(3, Link(5))))
>>> add(s, 3)
Link(0, Link(1, Link(3, Link(5))))
>>> add(s, 4)
Link(0, Link(1, Link(3, Link(4, Link(5)))))
>>> add(s, 6)
Link(0, Link(1, Link(3, Link(4, Link(5, Link(6))))))
"""
if new_val < ordered_list.first:
original_first = ordered_list.first
ordered_list.first = new_val
ordered_list.rest = Link(original_first, ordered_list.rest)
elif new_val > ordered_list.first and ordered_list.rest is Link.empty:
ordered_list.rest = Link(new_val)
elif new_val > ordered_list.first:
add(ordered_list.rest, new_val)
return ordered_list
Showdown: Python list vs. Link
The challenge:
- Store all the half-a-million words in "War and Peace"
- Insert a word at the beginning.
| Version | 10,000 runs | 100,000 runs |
|---|---|---|
| Python list | 2.6 seconds | 37 seconds |
| Link | 0.01 seconds | 0.1 |
Try it yourself on your local machine (Legit Python!): warandpeace.py
But, see our preformance comparison with other operators.
Trees
Tree concepts
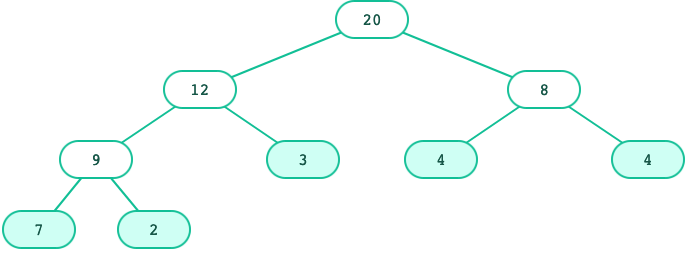
- A tree has a root label and a list of branches
- Each branch is itself a tree
- A tree with zero branches is called a leaf
Trees: Data abstraction
This is what we've been using:
tree(label, branches) |
Returns a tree with given LABEL at its root, whose branches are BRANCHES |
label(tree) |
Returns the label of root node of TREE |
branches(tree) |
Returns the branches of TREE (each a tree). |
is_leaf(tree) |
Returns true if TREE is a leaf node. |
Trees: Data abstraction
Using an implementation like this:
def tree(label, branches=[]):
return [label] + list(branches)
def label(tree):
return tree[0]
def branches(tree):
return tree[1:]
def is_leaf(tree):
return not branches(tree)
🤔 How could we represent trees as a Python class?
A Tree class
class Tree:
def __init__(self, label, branches=[]):
self.label = label
self.branches = list(branches)
def is_leaf(self):
return not self.branches
🤔 What's different? What's the same?
tree versus Tree
| tree | Tree |
|---|---|
t = tree(label, branches=[]) |
t = Tree(label, branches=[]) |
branches(t) |
t.branches
|
label(t) |
t.label
|
is_leaf(t) |
t.is_leaf() |
def fib_tree(n):
if n == 0 or n == 1:
return tree(n)
else:
left = fib_tree(n - 2)
right = fib_tree(n - 1)
fib_n = label(left) + label(right)
return tree(fib_n, [left, right])
def fib_tree(n):
if n == 0 or n == 1:
return Tree(n)
else:
left = fib_tree(n - 2)
right = fib_tree(n - 1)
fib_n = left.label + right.label
return Tree(fib_n, [left, right])
A fancier Tree
This is what assignments actually use:
class Tree:
def __init__(self, label, branches=[]):
self.label = label
for branch in branches:
assert isinstance(branch, Tree)
self.branches = list(branches)
def is_leaf(self):
return not self.branches
def __repr__(self):
if self.branches:
branch_str = ', ' + repr(self.branches)
else:
branch_str = ''
return 'Tree({0}{1})'.format(self.label, branch_str)
def __str__(self):
return '\n'.join(self.indented())
def indented(self):
lines = []
for b in self.branches:
for line in b.indented():
lines.append(' ' + line)
return [str(self.label)] + lines
Tree mutation
Doubling a Tree
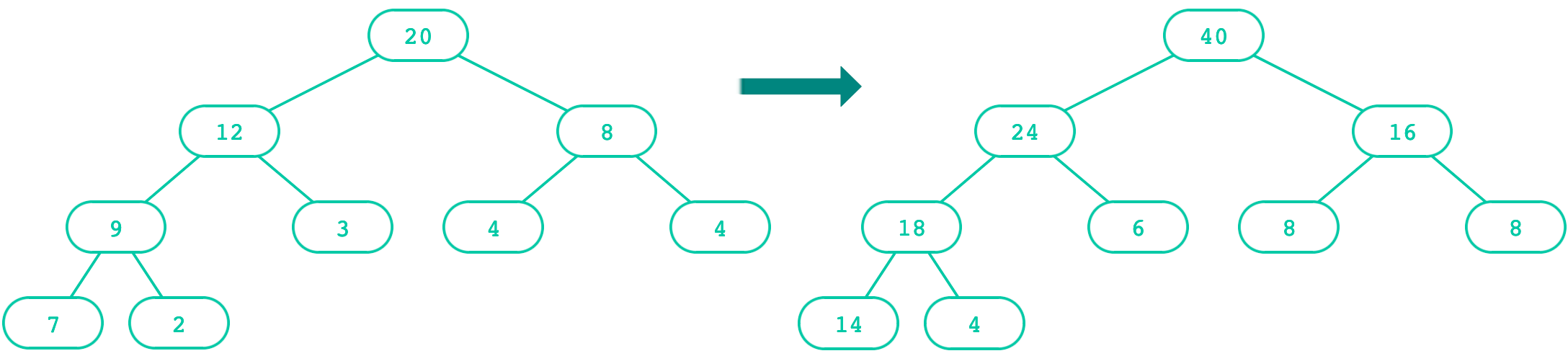
def double(t):
"""Doubles every label in t, mutating t.
>>> t = Tree(1, [Tree(3, [Tree(5)]), Tree(7)])
>>> double(t)
>>> t
Tree(2, [Tree(6, [Tree(10)]), Tree(14)])
"""
t.label = t.label * 2
for b in t.branches:
double(b)
Exercise: Pruning trees
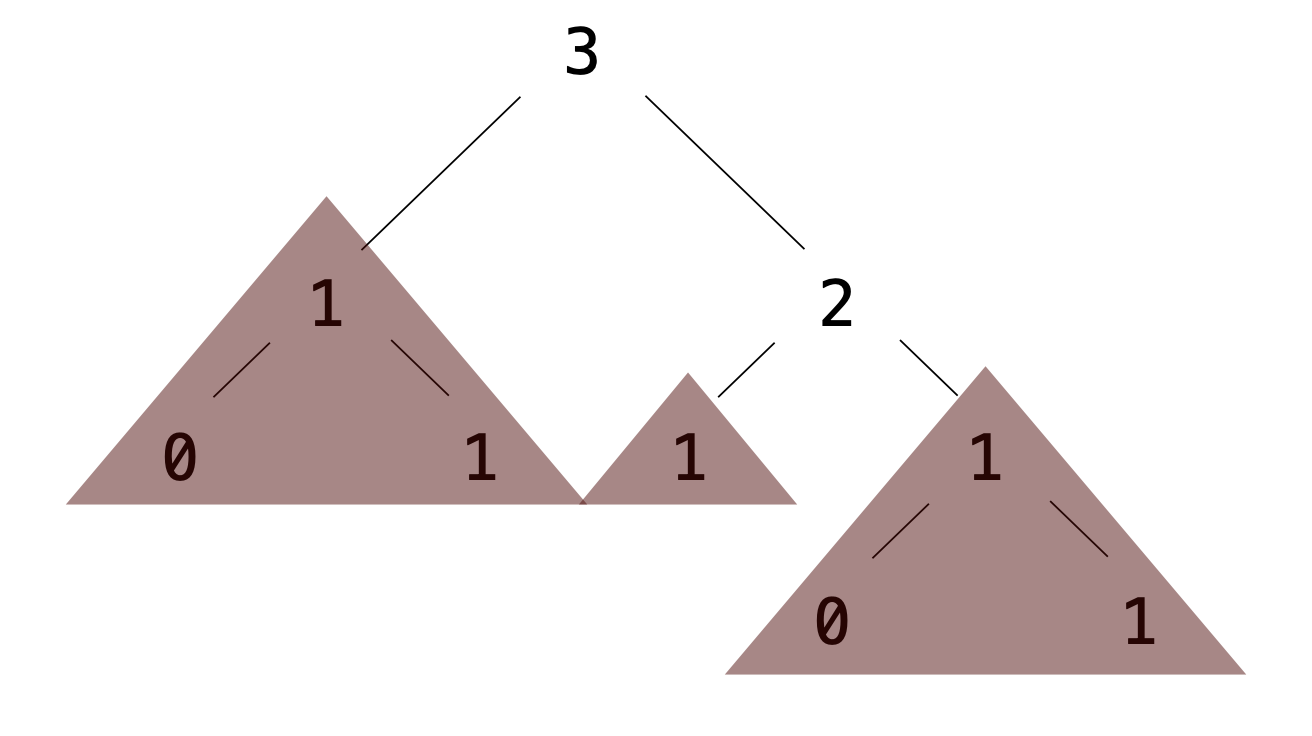
Removing subtrees from a tree is called pruning.
Always prune branches before recursive processing.
def prune(t, n):
"""Prune all sub-trees whose label is n.
>>> t = Tree(3, [Tree(1, [Tree(0), Tree(1)]), Tree(2, [Tree(1), Tree(1, [Tree(0), Tree(1)])])])
>>> prune(t, 1)
>>> t
Tree(3, [Tree(2)])
"""
t.branches = [___ for b in t.branches if ___]
for b in t.branches:
prune(___, ___)
Exercise: Pruning trees (Solution)

Removing subtrees from a tree is called pruning.
Always prune branches before recursive processing.
def prune(t, n):
"""Prune all sub-trees whose label is n.
>>> t = Tree(3, [Tree(1, [Tree(0), Tree(1)]), Tree(2, [Tree(1), Tree(1, [Tree(0), Tree(1)])])])
>>> prune(t, 1)
>>> t
Tree(3, [Tree(2)])
"""
t.branches = [b for b in t.branches if b.label !=n]
for b in t.branches:
prune(b, n)
Recursive objects
Why are Tree and Link considered recursive
objects?
Each type of object contains references to the same type of object.
-
An instance of
Treecan contain additional instances ofTree, in thebranchesvariable. -
An instance of
Linkcan contain an additional instance ofLink, in therestvariable.
Both classes lend themselves to recursive algorithms. Generally:
-
For
Tree: The base case is whenis_leaf()is true;
the recursive call is on thebranches. -
For
Link: The base case is when the rest isempty;
the recursive call is on therest.