Efficiency

Tips for navigating the slides:
  • Press O or Escape for overview mode.
  • Press the copy icon on the upper right of code blocks to copy the code

Class outline:

  • Exponentiation
  • Orders of Growth
  • Memoization

Exponentiation

Exponentiation approach #1

Based on this recursive definition:

$$\begin{equation*} b^n= \begin{cases} 1 & \text{if } n = 0 \\ b \cdot b^{(n-1)} & \text{otherwise} \\ \end{cases} \end{equation*}$$ 


                    def exp(b, n):
                      if n == 0:
                        return 1
                      else:
                        return b * exp(b, n-1)

How many calls are required to calculate exp(2, 16)?

Can we do better?

Exponentiation approach #2

Based on this alternate definition:

$$\begin{equation*} b^n= \begin{cases} 1 & \text{if } n = 0 \\ (b^{\frac{1}{2}n})^2 & \text{if $n$ is even} \\ b \cdot b^{(n-1)} & \text{if $n$ is odd} \\ \end{cases} \end{equation*}$$ 


                    def exp_fast(b, n):
                        if n == 0:
                            return 1
                        elif n % 2 == 0:
                            return square(exp_fast(b, n//2))
                        else:
                            return b * exp_fast(b, n-1) 
                    
                    square = lambda x: x * x

How many calls are required to calculate exp(2, 16)?

Some algorithms are more efficient than others!

Orders of Growth

Common orders of growth

One way to describe the efficiency of an algorithm according to its order of growth, the effect of increasing the size of input on the number of steps required.

Order of growth Description
Exponential growth Number of steps increases faster than a polynomial function of the input size.
Quadratic growth Number of steps increases in proportion to the square of the input size.
Linear growth Number of steps increases in direct proportion to the input size.
Logarithmic growth Number of steps increases proportionally to the logarithm of the input size.
Constant growth Always takes same number of steps, regardless of input size.

Adding to the front of linked list


                    def insert_front(linked_list, new_val):
                        """Inserts NEW_VAL in front of LINKED_LIST,returning new linked list.
                        >>> ll = Link(1, Link(3, Link(5)))
                        >>> insert_front(ll, 0)
                        Link(0, Link(1, Link(3, Link(5))))
                        """
                        return Link(new_val, linked_list)

How many operations will this require for increasing lengths of the list?

List size Operations
1 1
10 1
100 1
1000 1

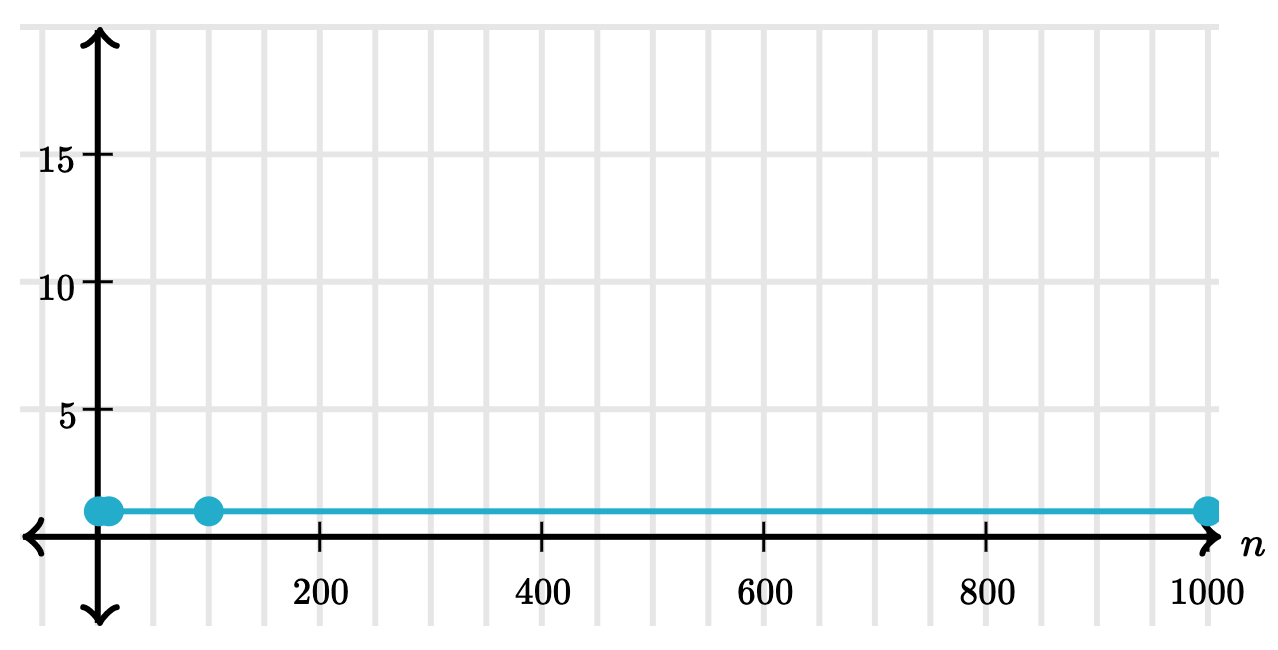
Constant time

An algorithm that takes constant time, always makes a fixed number of operations regardless of the input size.

List size Operations
1 1
10 1
100 1
1000 1
Graph of constant time

Fast exponentiation


                    def exp_fast(b, n):
                        if n == 0:
                            return 1
                        elif n % 2 == 0:
                            return square(exp_fast(b, n//2))
                        else:
                            return b * exp_fast(b, n-1) 
                    
                    square = lambda x: x * x

How many operations will this require for increasing values of n?

N Operations
0 1
8 5
16 6
1024 12

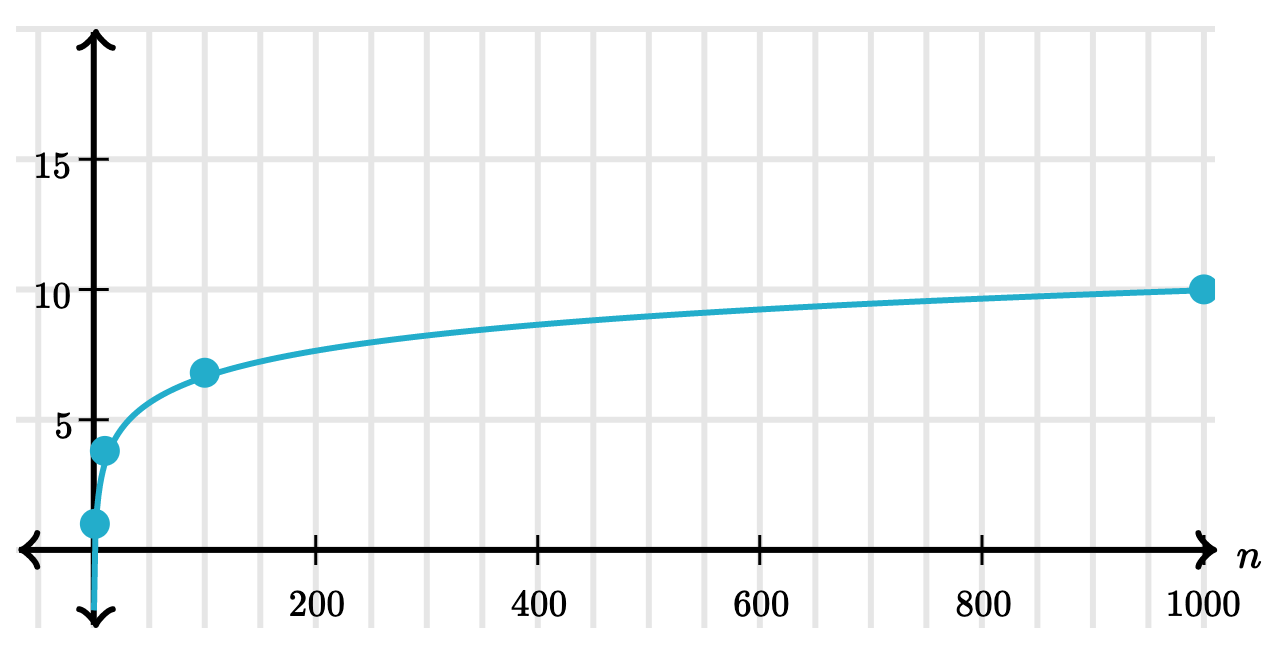
Logarithmic time

When an algorithm takes logarithmic time, the time that it takes increases proportionally to the logarithm of the input size.

N Operations
0 1
8 5
16 6
1024 12
Graph of logarithmic time

Finding value in a linked list


                    def find_in_link(ll, value):
                        """Return true if linked list LL contains VALUE.
                        >>> find_in_link(Link(3, Link(4, Link(5))), 4)
                        True
                        >>> find_in_link(Link(3, Link(4, Link(5))), 7)
                        False
                        """
                        if ll is Link.empty:
                            return False
                        elif ll.first == value:
                            return True
                        return find_in_link(ll.rest, value)

How many operations will this require for increasing lengths of the list? Consider both the best case and worst case.

List size Best case: Operations Worst case: Operations
1 1 1
10 1 10
100 1 100
1000 1 1000

Linear time

When an algorithm takes linear time, its number of operations increases in direct proportion to the input size.

List size Worst case: Operations
1 1
10 10
100 100
1000 1000
Graph of linear time

Counting overlapping items in lists


                        def overlap(a, b):
                            """
                            >>> overlap([3, 5, 7, 6], [4, 5, 6, 5])
                            3
                            """
                            count = 0
                            for item in a:
                                for other in b:
                                    if item == other:
                                        count += 1
                            return count
3 5 6 7
4
5 +
6 +
5 +

How many operations are required for increasing lengths of the lists?

List size Operations
1 1
10 100
100 10000
1000 1000000

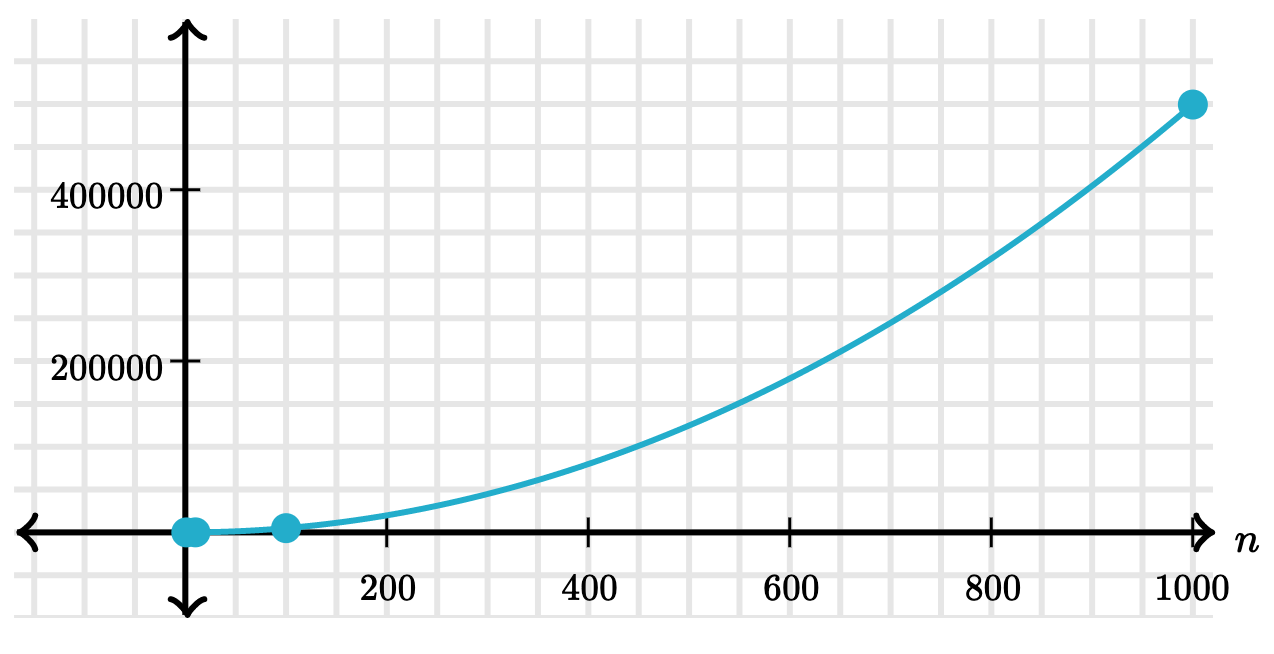
Quadratic time

When an algorithm grows in quadratic time, its steps increase in proportion to square of the input size.

List size Operations
1 1
10 100
100 10000
1000 1000000
Graph of quadratic time

Recursive Virahanka-Fibonacci


                    def virfib(n):
                      if n == 0:
                        return 0
                      elif n == 1:
                        return 1
                      else:
                        return virfib(n-2) + virfib(n-1)

How many operations are required for increasing values of n?

N Operations
1 1
2 3
3 5
4 9
7 41
8 67
20 21891

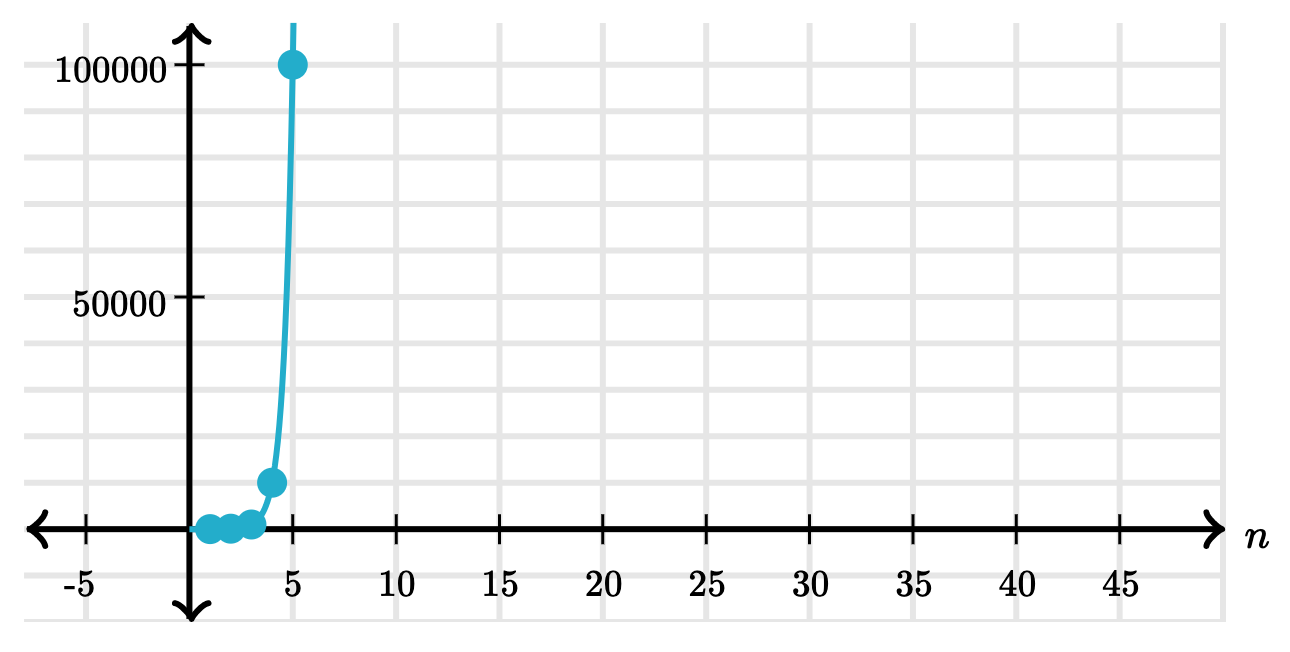
Exponential time

When an algorithm grows in exponential time, its number of steps increases faster than a polynomial function of the input size.

N Operations
1 1
2 3
3 5
4 9
7 41
8 67
20 21891
Graph of exponential time

Comparing orders of growth

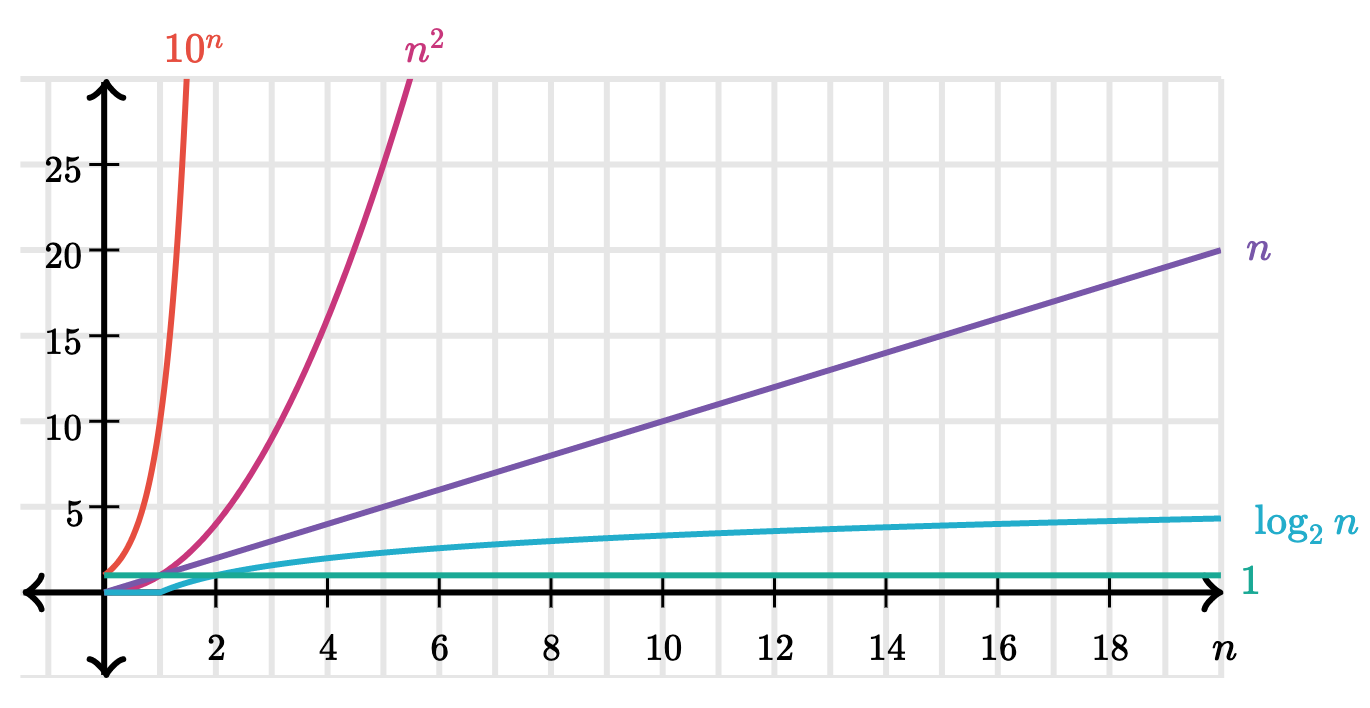
graph of all orders of growth overlaid

Big O Notation

A formal notation for describing the efficiency of an algorithm, using asymptotic analysis.

Order of growth Example Big O
Exponential growth recursive virfib $$O(b^n)$$
Quadratic growth overlap $$O(n^2)$$
Linear growth find_in_link $$O(n)$$
Logarithmic growth exp_fast $$O(\log n)$$
Constant growth add_to_front $$O(1)$$

Space

Space and environments

The space needed for a program depends on the environments in use.

At any moment there is a set of active environments.

Values and frames in active environments consume memory.

Memory that is used for other values and frames can be recycled.

Active environments:

  • Environments for any function calls currently being evaluated.
  • Parent environments of functions named in active environments.

Active environments in PythonTutor


                    def virfib(n):
                        if n == 0:
                            return 0
                        elif n == 1:
                            return 1
                        else:
                            return virfib(n-2) + virfib(n-1)

View in PythonTutor
Make sure to select "don't display exited functions".

Visualization of space consumption

140268980982768 virfib(3) 140269249414448 virfib(4) 140268980983296 virfib(1) 140268980982768->140268980983296 140268980982768->140268980983296:c 1 140268177100928 virfib(2) 140268980982768->140268177100928 140268980982768->140268177100928:c 1 140269251956160 virfib(2) 140269249414448->140269251956160 140269249414448->140269251956160:c 1 140269251957216 virfib(3) 140269249414448->140269251957216 140269249414448->140269251957216:c 2 140268980984160 virfib(0) 140268177100928->140268980984160 140268177100928->140268980984160:c 0 140268980984688 virfib(1) 140268177100928->140268980984688 140268177100928->140268980984688:c 1 140268177101456 virfib(0) 140269251956160->140268177101456 140269251956160->140268177101456:c 0 140269251956688 virfib(1) 140269251956160->140269251956688 140269251956160->140269251956688:c 1 140268177102560 virfib(1) 140269251957216->140268177102560 140269251957216->140268177102560:c 1 140269251957744 virfib(2) 140269251957216->140269251957744 140269251957216->140269251957744:c 1 140269251958272 virfib(0) 140269251957744->140269251958272 140269251957744->140269251958272:c 0 140269249414976 virfib(1) 140269251957744->140269249414976 140269251957744->140269249414976:c 1 140269251955632 virfib(5) 140269251955632->140268980982768 140269251955632->140268980982768:c 2 140269251955632->140269249414448 140269251955632->140269249414448:c 3 99999999 Result 99999999->140269251955632:c 5

Memoization

Memoization

Memoization is a strategy to reduce redundant computation by remembering the results of previous function calls in a "memo".

A memoization HOF


                    def memo(f):
                        cache = {}
                        def memoized(n):
                            if n not in cache:
                                cache[n] = f(n)
                            return cache[n]
                        return memoized

Memoizing Virahanka-Fibonacci

n Original Memoized
5 15 9
6 25 11
7 41 13
8 67 15
9 109 17
10 177 19
Video visualization